Sometimes during data analysis, it becomes useful to perform a rolling calculation, also referred to as a running calculation or a moving calculation.

These types of calculations are relatively easy to perform with standard Excel formulas. For example, with a rolling maximum calculation the formula simply compares the current value against the previous maximum value.

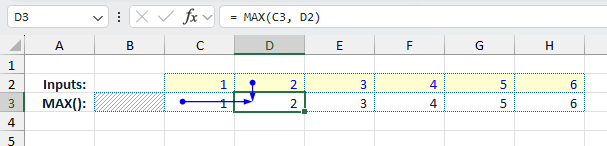
As this style of calculation often requires looking back at the previous period output/answer, this can be difficult to implement with dynamic arrays. This is because with Dynamic Arrays, the whole array is calculated in a single step and then output (“spilled”) across the required number of worksheet cells. As such, looking back at a previous output value within the same calculation creates a circular reference.

This circular reference issue can be solved with the use of one of the newer Dynamic Array helper functions, the SCAN() function.

The SCAN() function, takes a starting value and an array, and then traverses that array from left-to-right, top-to-bottom (i.e. by column and then by row / across each row before moving down to the next row). Within the SCAN() function, the actual calculation is performed using a LAMBDA() function which takes two arguments:

• the accumulated output value (_acc in the examples below); and
• the current value from the input array (_val in the examples below)

= SCAN([initial_value], [input_array], LAMBDA([_acc],[_val], [calculation))

In this way, for a rolling maximum calculation, as the SCAN() function considers each value in the input array it can be compared against the previous calculated result, and the new maximum value is calculated and output.

Rolling Calculations with Dynamic Arrays

One of the advantages of Dynamic Arrays (DA) is their flexibility and their being dynamic(!). As list of input values changes, including increasing/decreasing in number or expanding/contracting in dimensions on the worksheet, by using dynamic arrays as calculation references there is no need to manually update your formulae. Particularly when it comes to staged calculations – where the end-point calculation in your analysis relies on prior calculations rather than directly referencing the inputs – by using a dynamic reference to your inputs and then DA references in all of the calculations, there is no need to update the formulae as the inputs are updated.

As discussed above, the SCAN() function is very helpful here to be able to create such rolling calculations that will work well with arrays, especially DAs. But once any additional functionality is included, such as ignoring blank cells, zero values, non-numeric values, or errors, the calculations can become rather complex and long to write. As such, I wanted to develop dynamic and flexible methods for calculating some common rolling calculations which could then be combined into a single custom LAMBDA() function meaning I wouldn’t need to re-write these formulae each time I wanted to use a rolling calculation.

Rolling SUM()

A rolling SUM() function should be simple to produce as it just requires moving along the input array and adding the current value to the previously calculated total.

With standard (non-DA) Excel formulae this is simple enough to achieve. However, the SUM() function is designed to return a single result making this is more complicated for DAs, as the full array will be input to the SUM() function and then summated together rather than producing the rolling total at each point in the input array.

If instead the addition operator (+) is used between two input arrays (inc. DAs), this will add together the arrays, matching values of the same index in each array, to give a single DA output.

As mentioned above, it is not possible to reference back to the previous calculated result from a DA when calculating that DA output as the full array needs to be calculated before it is output and referenceable, and so this creates a circular reference.

This is where the SCAN() function comes into its own, as it allows for a temporary output variable (the accumulated value variable in the SCAN() function’s LAMBDA()) to be used to store the output result at each stage of the calculation. This temporary variable can be referenced within the main calculation without creating a circular reference as it is effectively separate.

At its simplest, a rolling SUM() function can be created via a simple addition (+ operator) within the LAMBDA() function of the SCAN() to add the accumulated value and the current value. Alternatively, the SUM() function can be used to achieve the same result, and since the introduction of eta-reduced DA helper functions, you can simply replace the LAMBDA() function within the SCAN() function with a direct reference to the function you wish to perform — i.e. just typing SUM as shown below. This means that you don’t need to type out the full LAMBDA() function yourself.

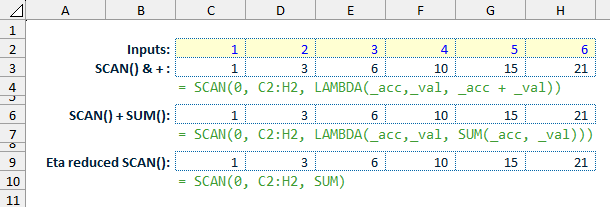
By using the simple + operator and adding some additional logic to the SCAN() function, it is possible to include the intended functionality of being able to ignore non-numeric values, blank cells, and error cells when calculating the rolling total.

// Rolling SUM
= SCAN(0, [input array], 
    LAMBDA(_acc,_val, 
        _acc + IF( OR( ISERROR(_val), ISBLANK(_val), NOT(ISNUMBER(_val))), 0, _val)
    )
)

Rolling COUNT()

Similar to the SUM() function, the COUNT() function will only return a single output result when provided with an array of input values. Again, the SCAN() function can be used to create a rolling calculation as the input array is traversed. However, when simply using the COUNT() function within the LAMBDA() section of the SCAN() function, especially if using the eta-reduced COUNT keyword, the result is not as might be expected.

This is because, the COUNT() function takes the two LAMBDA() variables (_acc and _val) and counts the number of numeric values between these two variables. The accumulated output value (_acc) is just a single value used as a temporary variable at each stage of the SCAN() main calculation, and the current value accessed by the main SCAN() calculation (_val) is also a single value; in this case the starting value (0) is also a single numeric value. Therefore, at each stage of the main SCAN() calculation, the COUNT() function is only considering two values, meaning that the answer is 2 at each stage.

To change this, you can create your own simple counting logic and then use the SCAN() output to keep a tally of your count.

This also allows for inclusion of the additional logic for the added functionality to exclude zero values, error values, and blank cells from the calculation as wanted as well as only including numeric values like the native COUNT() function.

// Rolling COUNT
= SCAN(0, [input array], 
    LAMBDA(_acc,_val, 
        _acc + IF( AND(NOT(ISERROR(_val)), NOT(ISBLANK(_val)), ISNUMBER(_val), IFERROR(_val, 0) <> 0), 1, 0)
    )
)

Rolling AVERAGE()

For an accurate rolling/moving average, the average needs to consider all previous values at each stage of the calculation, rather than simply looking back to the previous calculated average and then using that value and the current value to get a new average. With standard Excel formulae this can be achieved easily by using a moving cell reference in the AVERAGE() function with the initial cell reference anchored. However, again the AVERAGE() function returns a single value as the result, and so this approach is not dynamic and will not work for an array, especially a DA, in the manner intended.

Instead, we can use the SCAN() function with one of two potential approaches.

1. Use the SCAN() function to traverse the dimensions of the input array rather than the values of the input array and use this to drive an AVERAGE() function.

• This approach is effective and if used with an AVERAGEIFS() function would allow for the extended functionality (e.g. ignoring zero values, blank cells, etc.). However, it is more complicated to keep fully flexible if allowing for the input array to be either vertically (multiple columns) or horizontally (multiple rows) aligned.

2. Use the SCAN() function with manual average calculation to mimic the result of an anchored, moving range AVERAGE() function.

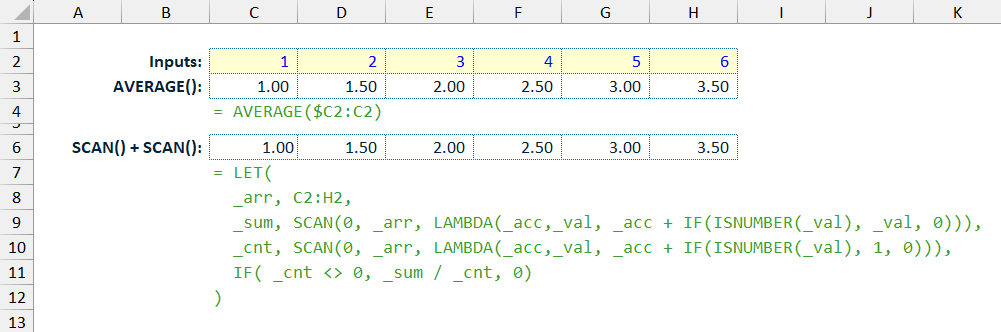
As I am intending on keeping my custom function as flexible and extendable as possible, and I am already developing methods to calculate the SUM and COUNT of the input array (as described above), I decided to go with the second option.

// Rolling AVERAGE -- uses the rolling SUM and COUNT methods from above within a LET() function
= LET(
    _arr, [input array],
    _sum, SCAN(0, _arr, LAMBDA(_acc,_val, _acc + IF(AND(NOT(ISERROR(_val)), NOT(ISBLANK(_val)), IFERROR(_val, 0) <> 0), _val, 0))),
    _cnt, SCAN(0, _arr, LAMBDA(_acc,_val, _acc + IF(AND(NOT(ISERROR(_val)), NOT(ISBLANK(_val)), IFERROR(_val, 0) <> 0), 1, 0))),
    IF(_cnt <> 0, _sum / _cnt, 0)
)

Rolling MIN() & Rolling MAX()

For a rolling maximum or minimum value, the calculation required is relatively simple – compare the previous max/min value against the current and output the result. As such, the SCAN() function is ideal as the accumulated/previous output value in the LAMBDA() function can be compared directly against the current input array value using the MAX() or MIN() functions.

When adding the extra functionality of being able to exclude, zero values, blank cells, error cells, and non-numeric values, this is also simple to complete with either some extended logic in the LAMBDA() section of the SCAN() function or by using a MAXIFS() or MINIFS() function in the LAMBDA().

The complication can instead be setting the SCAN() function initial value, as this is a mandatory input parameter for the SCAN() function. For the rolling SUM and rolling COUNT examples above, this input has simply been set to zero (0). However, this could cause incorrect results with the MAX() and MIN() functions:

• If the initial SCAN() function value is 0 and the first input value is 1, then MIN() function comparison of the two would incorrectly give a result of 0 -> the correct result should be 1, as this is the first value in the rolling calculation and so has to be the minimum value in a data set of one value.

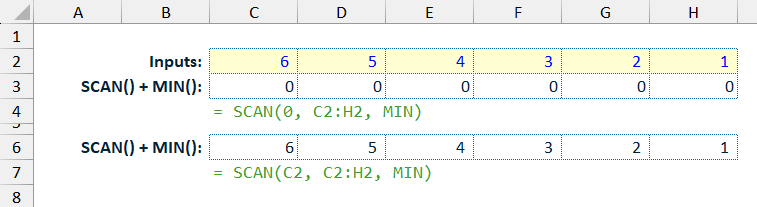
• If the initial SCAN() function value is 0 and the first input value is -1, then MAX() function comparison of the two would incorrectly give a result of 0 -> the correct result should be -1, as this is the first value in the rolling calculation and so has to be the maximum value in a data set of one value.

My solution is to find the first appropriate value in the input data set and use this as the SCAN() function initial value, which can be complicated if excluding any non-numeric values, blank cells, error cells, etc.

• e.g. if the first value in the input array is 1, then the SCAN() function initial value is set to 1, meaning that the first MIN()/MAX() comparison of the main calculation would be comparing 1 against 1.

// Rolling MIN
= SCAN( INDEX([input array], 1, 1), [input array], 
    LAMBDA(_acc,_val, 
        IF( AND(NOT(ISERROR(_val)), NOT(ISBLANK(_val)), IFERROR(_val, 0) <> 0), MIN(_acc, _val), _acc)
    )
)
// Rolling MAX
= SCAN( INDEX([input array], 1, 1), [input array], 
    LAMBDA(_acc,_val, 
        IF( AND(NOT(ISERROR(_val)), NOT(ISBLANK(_val)), IFERROR(_val, 0) <> 0), MAX(_acc, _val), _acc)
    )
)

Custom LAMBDA() function

Having developed ways of dynamically and flexibly calculating my chosen five rolling calculations, the next step is to combine them into a single custom LAMBDA() function, with the user having the ability to choose which output they want. I have also added the ability to exclude blank input cells (using the ignore_blanks input parameter), zero values in the input array (using the ignore_zeros input parameter), and to ignore all error values (using the ignore_errors input parameter).

Note: By default, the function will exclude any #N/A values within the input array from the rolling calculations; any other error values (“# values”) will not be excluded so that potential errors in the input array will follow through to the function output and alert the user. To exclude all errors from the function calculations, use the ignore_errors input parameter.

The custom function is designed to be flexible enough to accept a single dimension (1D) input array (array input parameter) in either vertical or horizontal orientation. By default, the function will return its output array in the same orientation as the input array but can be forced to be output as either a vertical or horizontal array (using the vertical_output input parameter).

To make the custom function more user friendly, the user can enter the calculation input parameter as either a number from 1 to 5 or as short text string (not case sensitive) from an expected list:

RCalc() function

Below is the final combined RCalc() function:

= LAMBDA(
  // Parameter declarations
  array,
  calculation,
  [ignore_blanks],
  [ignore_zeros],
  [ignore_errors],
  [vertical_output],
  // Main function body/calculations
  LET(
    // Deal with the calculation parameter input and attempt to match against expected text inputs if the
    // input is not a number
    _num, IF( ISNUMBER(calculation), calculation, IFERROR( MATCH(LOWER(calculation), {"sum","count","avg","min","max"}, 0), 0)),
    // Deal with the optional input parameters and set default values for any omitted parameters
    _igB, IF( ISOMITTED(ignore_blanks), 0, ignore_blanks),
    _igZ, IF( ISOMITTED(ignore_zeros), 0, ignore_zeros),
    _igE, IF( ISOMITTED(ignore_errors), 0, ignore_errors),
    _vOut, IF( ISOMITTED(vertical_output), -1, IF(vertical_output, 1, 0)),
    // Check input validity
    //  --> invalid array input (not a 1D array) will give a #CALC! error
    //  --> invalid calculation, ignore_blanks, or ignore_zeros parameter inputs will give a #VALUE! error
    _inpChk, IF( OR(
      AND( ROWS(array) > 1, COLUMNS(array) > 1),
      ROWS(array) < 1, COLUMNS(array) < 1),
      2,
      IF( OR(
        AND( NOT(ISLOGICAL(_igB)), NOT(ISNUMBER(_igB))),
        AND( NOT(ISLOGICAL(_igZ)), NOT(ISNUMBER(_igZ))),
        AND( NOT(ISLOGICAL(_igE)), NOT(ISNUMBER(_igE))),
        _num < 1, _num > 5),
        3, 1
      )
    ),
    // Determine the orientation of the input data array
    _vrt, ROWS(array) > COLUMNS(array),
    // Filter the input data array for error values, blank cells, and zero (0) values
    _fltE, IF(_igE, IF( ISERROR(array), " ", array), IFNA(array, " ")),
    _fltB, IF(_igB, IF( ISBLANK(array), " ", _fltE), _fltE),
    _fltZ, IF(_igZ, IF((--NOT(ISERROR(array)) * --NOT(ISBLANK(array)) * --(IFERROR(array, " ") = 0)), " ", _fltB), _fltB),
    // Set the initial value for the rolling MIN and MAX calculations
    //  --> uses the value in the array -- if this is not a number then the #N/A is used instead
    //  --> for the SUM, COUNT, and AVERAGE calculations, the starting value is 0 (zero)
    _fst, INDEX(_fltZ, 1, 1),
    _init, IF((--(_fst <> " ") * --NOT(ISBLANK(_fst)) * --(IFERROR(_fst, " ") = 0)), _fst, NA()),
    // Calculate the rolling SUM and COUNT values to be used for the SUM, COUNT, or AVERAGE outputs
    _sum, IF( OR(_num = 1, _num = 3),
      SCAN(0, _fltZ, LAMBDA(_acc,_val, _acc + IF( ISNUMBER(_val), _val, 0))),
      ""
    ),
    _cnt, IF( OR(_num = 2, _num = 3),
      SCAN(0, _fltZ, LAMBDA(_acc,_val, _acc + IF( ISNUMBER(_val), 1, 0))),
      ""
    ),
    // Calculate the chosen output based on the user selected calculation input parameter
    _out, CHOOSE(_num,
      _sum,
      _cnt,
      IF(_cnt <> 0, _sum / _cnt, 0),
      SCAN(_init, _fltZ, LAMBDA(_acc,_val, IFS( AND( ISNA(_acc), ISNUMBER(_val)), _val, ISNUMBER(_val), MIN(_acc, _val), TRUE, _acc))),
      SCAN(_init, _fltZ, LAMBDA(_acc,_val, IFS( AND( ISNA(_acc), ISNUMBER(_val)), _val, ISNUMBER(_val), MAX(_acc, _val), TRUE, _acc)))
    ),
    // Determine whether to force a particular output orientation and transpose the calculated output 
    // as required
    _rtn, IFS(
      _vOut < 0, _out,
      OR(
        AND(_vOut, NOT(_vrt)),
        AND(NOT(_vOut), _vrt)
      ),
      TRANSPOSE(_out),
      TRUE, _out
    ),
    // If the input checks (_inpChk) have flagged then return the required Excel error code, otherwise 
    // return the calculated result (_rtn)
    CHOOSE(_inpChk, _rtn, LAMBDA(0), #VALUE!)
  )
)

The function starts by dealing with the calculation input value and determining if a non-number value is passed whether it is one of the expected and allowed text inputs (line 13). This is followed by assessing the optional input parameters and setting default values if any have been omitted by the user (lines 15-18).

Next there is an IF() block which is used to perform input checks. This ensures that the input array passed is valid, the calculation input passed is valid (either a number between 1 and 5 or an allowed string), and that the optional parameter values passed are either a TRUE/FALSE Boolean value or a number (lines 22-33).

The orientation of the initial input array is determined so that the correct orientation can be applied to the output as required (line 35).

To make the combined calculation more efficient, the array of input values (array) is filtered to exclude non-#N/A error values, blank cells, and zero values (_fltZ), as per the optional user inputs (ignore_errors, ignore_blanks, ignore_zeros) rather than including this logic in each of the individual main calculations (lines 37-39). The initial value to be used for the rolling MIN and rolling MAX calculations (_init) is also set (lines 43-44).

The main calculations are performed using broadly the approaches described above and based on the SCAN() function. If the user has selected a rolling SUM or AVERAGE output, then the rolling SUM output is calculated (_sum, lines 46-49). If the user has selected a rolling COUNT or AVERAGE output, then the rolling COUNT output is calculated (_cnt, lines 50-53). The output calculation (_out) is then determined with a CHOOSE() function (lines 55-61)

• if the user has selected a rolling SUM or COUNT output the already calculated output is used (_sum or _cnt);
• if a rolling AVERAGE output is selected then this is calculated using the SUM and COUNT outputs that have already been calculated (_sum/_cnt);
• if a rolling MIN or MAX output is selected then this is calculated using the SCAN() function approach as above.

Having chosen and calculated the required output array, the function determines whether the output array orientation needs to be changed to fit with the user input (lines 64-72).

Finally, the function checks whether an input check was flagged (line 75), in which case the appropriate Excel error code is returned as the final function output, otherwise the updated calculated output array (_rtn) is returned.

If you want to use the RCalc() function in your own projects or custom functions, please use one of the options below:

1. Using Excel Labs Advanced Formula Environment (AFE) download the RXL_RCalc function using the Gist URL https://gist.github.com/r-silk/b124f8468b1615a40b42feda7545bc0a
2. Alternatively, go to the GitHub repository https://github.com/r-silk/RXL_Lambdas and download the file RXL_RCalc.xlsx
   • this file contains a copy of the function in the Defined Names which can be copied into your own file
   • there is also a “minimised” version of the function which can be copied and pasted directly into the Name Manager when defining a new name of your own — please use the suggested function name of RXL_RCalc
   • the available file contains the documentation for the function as well as some details on development and testing/example usage